Example: DC-DC converter solved by Uniform grid abstraction.

We consider a boost DC-DC converter which has been widely studied from the point of view of hybrid control, see for example in [1, V.A],[2],[3]. This is a safety problem for a switching system.

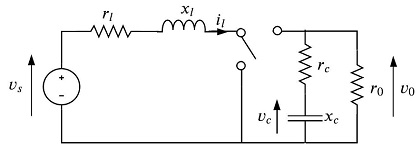
The state of the system is given by $x(t) = \begin{bmatrix} i_l(t) & v_c(t) \end{bmatrix}^\top$. The switching system has two modes consisting in two-dimensional affine dynamics:

\[\dot{x} = f_p(x) = A_p x + b_p,\quad p=1,2\]

with

\[A_1 = \begin{bmatrix} -\frac{r_l}{x_l} &0 \\ 0 & -\frac{1}{x_c}\frac{1}{r_0+r_c} \end{bmatrix}, A_2= \begin{bmatrix} -\frac{1}{x_l}\left(r_l+\frac{r_0r_c}{r_0+r_c}\right) & -\frac{1}{x_l}\frac{r_0}{r_0+r_c} \\ \frac{1}{x_c}\frac{r_0}{r_0+r_c} & -\frac{1}{x_c}\frac{1}{r_0+r_c} \end{bmatrix}, b_1 = b_2 = \begin{bmatrix} \frac{v_s}{x_l}\\0\end{bmatrix}.\]

The goal is to design a controller to keep the state of the system in a safety region around the reference desired value, using as input only the switching signal. In order to study the concrete system and its symbolic abstraction in a unified framework, we will solve the problem for the sampled system with a sampling time $\tau$. For the construction of the relations in the abstraction, it is necessary to over-approximate attainable sets of a particular cell. In this example, we consider the use of a growth bound function [4, VIII.2, VIII.5] which is one of the possible methods to over-approximate attainable sets of a particular cell based on the state reach by its center.

First, let us import StaticArrays and Plots.

using StaticArrays, JuMP, Plots

At this point, we import the useful Dionysos sub-modules.

using Dionysos
const DI = Dionysos
const UT = DI.Utils
const ST = DI.System
const MP = DI.Mapping
const SY = DI.Symbolic
const OP = DI.Optim
const AB = OP.Abstraction

Dionysos.Optim.Abstraction

Definition of the system

we can import the module containing the DCDC problem like this

include(joinpath(dirname(dirname(pathof(Dionysos))), "problems", "dc_dc.jl"));

and we can instantiate the DC system with the provided system

concrete_problem = DCDC.problem()
concrete_system = concrete_problem.system

x0 = SVector(0.0, 0.0)
hx = SVector(2.0 / 4.0e3, 2.0 / 4.0e3)
state_grid = MP.GridFree(x0, hx)
u0 = SVector(1)
hu = SVector(1)
input_grid = MP.GridFree(u0, hu)

optimizer = MOI.instantiate(AB.UniformGridAbstraction.Optimizer)
MOI.set(optimizer, MOI.RawOptimizerAttribute("concrete_problem"), concrete_problem)
MOI.set(optimizer, MOI.RawOptimizerAttribute("state_grid"), state_grid)
MOI.set(optimizer, MOI.RawOptimizerAttribute("input_grid"), input_grid)
MOI.set(optimizer, MOI.RawOptimizerAttribute("jacobian_bound"), DCDC.jacobian_bound())
MOI.set(optimizer, MOI.RawOptimizerAttribute("time_step"), 0.5)
MOI.set(
    optimizer,
    MOI.RawOptimizerAttribute("approx_mode"),
    AB.UniformGridAbstraction.GROWTH,
)
MOI.set(optimizer, MOI.RawOptimizerAttribute("efficient"), true)

MOI.optimize!(optimizer)

abstract_controller = MOI.get(optimizer, MOI.RawOptimizerAttribute("abstract_controller"))
concrete_controller = MOI.get(optimizer, MOI.RawOptimizerAttribute("concrete_controller"))
abstraction_time =
    MOI.get(optimizer, MOI.RawOptimizerAttribute("abstraction_construction_time_sec"))
println("Time to construct the abstraction: $(abstraction_time)")
abstract_problem_time =
    MOI.get(optimizer, MOI.RawOptimizerAttribute("abstract_problem_time_sec"))
println("Time to solve the abstract problem: $(abstract_problem_time)")
total_time = MOI.get(optimizer, MOI.RawOptimizerAttribute("solve_time_sec"))
println("Total time: $(total_time)")

invariant_set = MOI.get(optimizer, MOI.RawOptimizerAttribute("invariant_set"))
invariant_set_complement =
    MOI.get(optimizer, MOI.RawOptimizerAttribute("invariant_set_complement"));

[ Info: Number of states: 638401
[ Info: Number of inputs: 2
[ Info: Number of forward images: 1276802
┌ Warning: Noise is not yet accounted for in system abstraction.
└ @ Dionysos.Optim.Abstraction.UniformGridAbstraction ~/.julia/packages/Dionysos/LIv4k/src/optim/abstraction/UniformGridAbstraction/empty_problem.jl:649
compute_abstract_system_from_concrete_system!: started
[ Info: Starting sequential abstraction
┌ Info: Sequential abstraction progress
│   done = 100000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 200000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 300000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 400000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 500000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 600000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 700000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 800000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 900000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 1000000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 1100000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 1200000
└   total = 1276802
┌ Info: Finished sequential abstraction
│   total_work = 1276802
└   ntransitions = 3776873
compute_abstract_system_from_concrete_system! terminated with success: 3776873 transitions created
compute_controller_safe! started

 Safety: terminated with true
Time to construct the abstraction: 1.816673994064331
Time to solve the abstract problem: 0.5970711708068848
Total time: 2.413883924484253

Trajectory display

We choose the number of steps nsteps for the sampled system, i.e. the total elapsed time: nstep*tstep as well as the true initial state x0 which is contained in the initial state-space defined previously.

nstep = 300
x0 = SVector(1.2, 5.6)
x_traj, u_traj = ST.get_closed_loop_trajectory(
    MOI.get(optimizer, MOI.RawOptimizerAttribute("discrete_time_system")),
    concrete_controller,
    x0,
    nstep,
);

fig = plot(; aspect_ratio = :equal);
plot!(concrete_system.X; label = "", color = :grey);
plot!(concrete_problem.initial_set; color = :green, label = "");
plot!(x_traj; arrows = false, ms = 2.0, color = :blue)

Example: DC-DC converter solved by [Uniform grid abstraction] (https://github.com/dionysos-dev/Dionysos.jl/blob/master/docs/src/manual/manual.md#solvers) by exploiting the incremental stability of the system.

Definition of the system

we can import the module containing the DCDC problem like this

include(joinpath(dirname(dirname(pathof(Dionysos))), "problems", "dc_dc.jl"));

and we can instantiate the DC system with the provided system

concrete_problem = DCDC.problem()
concrete_system = concrete_problem.system

origin = SVector(0.0, 0.0)
η = (2 / 4.0) * 10^(-3);

Note: In the following, P and ϵ are computed by hand, but their computation is not crucial since they only affect the visualization of the abstraction. See https://github.com/dionysos-dev/Dionysos.jl/issues/345

ϵ = 0.1 * 0.01
P = SMatrix{2, 2}(1.0224, 0.0084, 0.0084, 1.0031)
state_grid = MP.GridEllipsoidalRectangular(origin, SVector(η, η), P / ϵ)

u0 = SVector(1)
hu = SVector(1)
input_grid = MP.GridFree(u0, hu)

optimizer = MOI.instantiate(AB.UniformGridAbstraction.Optimizer)
MOI.set(optimizer, MOI.RawOptimizerAttribute("concrete_problem"), concrete_problem)
MOI.set(optimizer, MOI.RawOptimizerAttribute("state_grid"), state_grid)
MOI.set(optimizer, MOI.RawOptimizerAttribute("input_grid"), input_grid)
MOI.set(optimizer, MOI.RawOptimizerAttribute("jacobian_bound"), DCDC.jacobian_bound())
MOI.set(
    optimizer,
    MOI.RawOptimizerAttribute("approx_mode"),
    AB.UniformGridAbstraction.CENTER_SIMULATION,
)
MOI.set(optimizer, MOI.RawOptimizerAttribute("time_step"), 0.5)
MOI.optimize!(optimizer);

abstract_system = MOI.get(optimizer, MOI.RawOptimizerAttribute("abstract_system"))
abstract_controller = MOI.get(optimizer, MOI.RawOptimizerAttribute("abstract_controller"))
concrete_controller = MOI.get(optimizer, MOI.RawOptimizerAttribute("concrete_controller"))
abstraction_time =
    MOI.get(optimizer, MOI.RawOptimizerAttribute("abstraction_construction_time_sec"))
println("Time to construct the abstraction: $(abstraction_time)")
abstract_problem_time =
    MOI.get(optimizer, MOI.RawOptimizerAttribute("abstract_problem_time_sec"))
println("Time to solve the abstract problem: $(abstract_problem_time)")
total_time = MOI.get(optimizer, MOI.RawOptimizerAttribute("solve_time_sec"))
println("Total time: $(total_time)")

[ Info: Number of states: 638401
[ Info: Number of inputs: 2
[ Info: Number of forward images: 1276802
┌ Warning: Noise is not yet accounted for in system abstraction.
└ @ Dionysos.Optim.Abstraction.UniformGridAbstraction ~/.julia/packages/Dionysos/LIv4k/src/optim/abstraction/UniformGridAbstraction/empty_problem.jl:649
compute_abstract_system_from_concrete_system!: started
[ Info: Starting sequential abstraction
┌ Info: Sequential abstraction progress
│   done = 100000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 200000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 300000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 400000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 500000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 600000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 700000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 800000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 900000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 1000000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 1100000
└   total = 1276802
┌ Info: Sequential abstraction progress
│   done = 1200000
└   total = 1276802
┌ Info: Finished sequential abstraction
│   total_work = 1276802
└   ntransitions = 932213
compute_abstract_system_from_concrete_system! terminated with success: 932213 transitions created
compute_controller_safe! started

 Safety: terminated with true
Time to construct the abstraction: 1.150001049041748
Time to solve the abstract problem: 0.40508389472961426
Total time: 1.5552160739898682

Trajectory display

We choose the number of steps nsteps for the sampled system, i.e. the total elapsed time: nstep*tstep as well as the true initial state x0 which is contained in the initial state-space defined previously.

nstep = 300
x0 = SVector(1.2, 5.6)
x_traj, u_traj = ST.get_closed_loop_trajectory(
    MOI.get(optimizer, MOI.RawOptimizerAttribute("discrete_time_system")),
    concrete_controller,
    x0,
    nstep,
)

Xmapping = SY.get_state_mapping(abstract_system)

fig = plot(; aspect_ratio = :equal);
plot!(concrete_system.X; label = "", color = :grey);
plot!(
    (invariant_set_complement, Xmapping);
    color = :black,
    label = "Invariant set complement",
)
plot!(concrete_problem.initial_set; color = :green, label = "");
plot!(x_traj; arrows = false, ms = 2.0, color = :blue)

References

1. A. Girard, G. Pola and P. Tabuada, "Approximately Bisimilar Symbolic Models for Incrementally Stable Switched Systems," in IEEE Transactions on Automatic Control, vol. 55, no. 1, pp. 116-126, Jan. 2010.
2. S. Mouelhi, A. Girard, and G. Gössler. “CoSyMA: a tool for controller synthesis using multi-scale abstractions”. In: HSCC. ACM. 2013, pp. 83–88.
3. A. Girard. “Controller synthesis for safety and reachability via approximate bisimulation”. In: Automatica 48.5 (2012), pp. 947–953.
4. G. Reissig, A. Weber and M. Rungger, "Feedback Refinement Relations for the Synthesis of Symbolic Controllers," in IEEE Transactions on Automatic Control, vol. 62, no. 4, pp. 1781-1796.

This page was generated using Literate.jl.